Introduction
- Confidence Level
Definition: The confidence level is a measure of the uncertainty or precision associated with a statistical estimate. It represents the probability that a confidence interval, calculated from a set of data, contains the true value of the parameter being estimated.
Commonly Used Levels: Confidence levels are often expressed as percentages, and a 95% confidence level is one of the most commonly used. A 95% confidence level implies that if we were to take many samples and create a confidence interval from each sample, we would expect about 95% of those intervals to contain the true population parameter.
- Standard Deviation:
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It indicates how much individual data points differ from the mean (average) of the data set. A low standard deviation suggests that the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range.
In statistical analysis, researchers often work with confidence intervals (CI) to estimate the range in which a true parameter value lies. This conversion tool is designed to calculate the standard deviation from a confidence interval, specifically for data collected from two distinct groups. The article explains the variables involved and the step-by-step process of how the standard deviation is derived from the provided confidence interval information.
Variables Definitions
- Upper CI Limit: The upper limit of the confidence interval for the data collected in both groups.
- Lower CI Limit: The lower limit of the confidence interval for the data collected in both groups.
- CI Level: The confidence interval level is expressed as a decimal value (e.g., 0.95 for a 95% confidence interval).
- Participants in Group 1: The number of participants in the first group.
- Participants in Group 2: The number of participants in the second group.
- Standard Deviation (SD): The calculated standard deviation based on the provided confidence interval information.
Conversion Formula
The calculation involves the following steps:
- Calculate the Standard Error Wide (seWide):

t-value - Calculate Standard Error (SE):
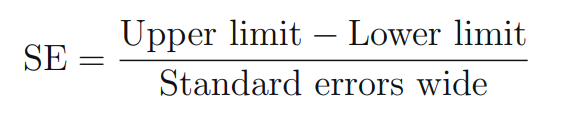
SE - Calculate Standard Deviation (SD):
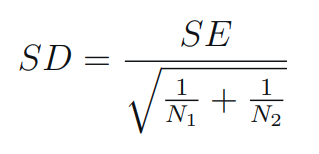
SD