Introduction
Analyzing individual patient data is crucial in healthcare and medical research. This article introduces a tool that facilitates the calculation of the mean and standard deviation for single patients' data. The tool is designed to handle both population and sample data, providing valuable insights into the central tendency and variability of the dataset.
Variables Definitions
- Patients' Data: A list of numerical values representing individual patient data, separated by commas (e.g., 5, 8, 13, 21).
- Sample Type (most common): A selection between "Population" and "Sample" data. This choice influences the calculation of the variance and, subsequently, the standard deviation.
- Population data is used when you want to describe the characteristics or parameters of an entire group. For example, the population of all adults in a country.
- Samples are used when it's impractical or impossible to collect data from an entire population. They provide a representation of the population.
- Sample Size: The total number of patients in the dataset.
- Mean: The average value of the patients' data.
- Standard Deviation (σ): A measure of the dispersion or spread of the patients' data.
- Variance: The squared standard deviation provides a measure of how much each number in the dataset differs from the mean.
- Sum: The sum of all values in the patients' data.
- Standard Error of the Mean (SEM): An estimate of the standard deviation of the sample mean, providing information about the precision of the mean estimate.
- The Margin of Error for Confidence Intervals: The margin of error at different confidence levels (68.3%, 90%, 95%, 99%, 99.9%, 99.99%, 99.999%, 99.9999%). These values help in understanding the range within which the true population mean is likely to fall.
Conversion Formula
The tool utilizes the following formulas to calculate the mean, standard deviation, and related metrics:
- Mean (μ): Calculated as the sum of all values divided by the number of patients.
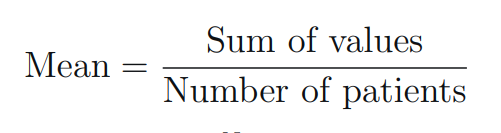
Mean - Variance (σ²): Calculated as the sum of squared differences between each value and the mean, divided by the total number of patients (for population data) or the number of patients minus one (for sample data).
- Population Standard Deviation:
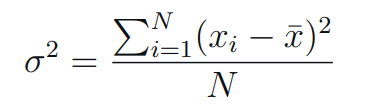
Variance for Population - Sample Standard Deviation:
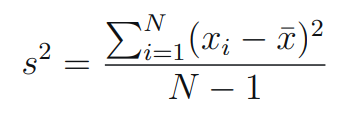
Variance for Sample
3. Standard Deviation (σ): The square root of the variance.
- Population Standard Deviation
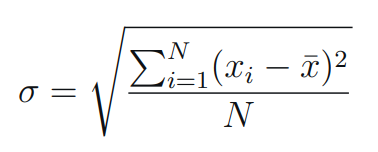
SD for Population
xi is an individual value
x̄ is the mean/expected value
N is the total number of values
- Sample Standard Deviation:
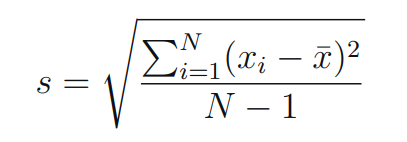
SD for Sample
xi is one sample value
x̄ is the sample mean
N is the sample size
- Standard Error of the Mean (SEM): Calculated as the standard deviation divided by the square root of the sample size.
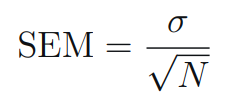
SEM
σ: standard deviation